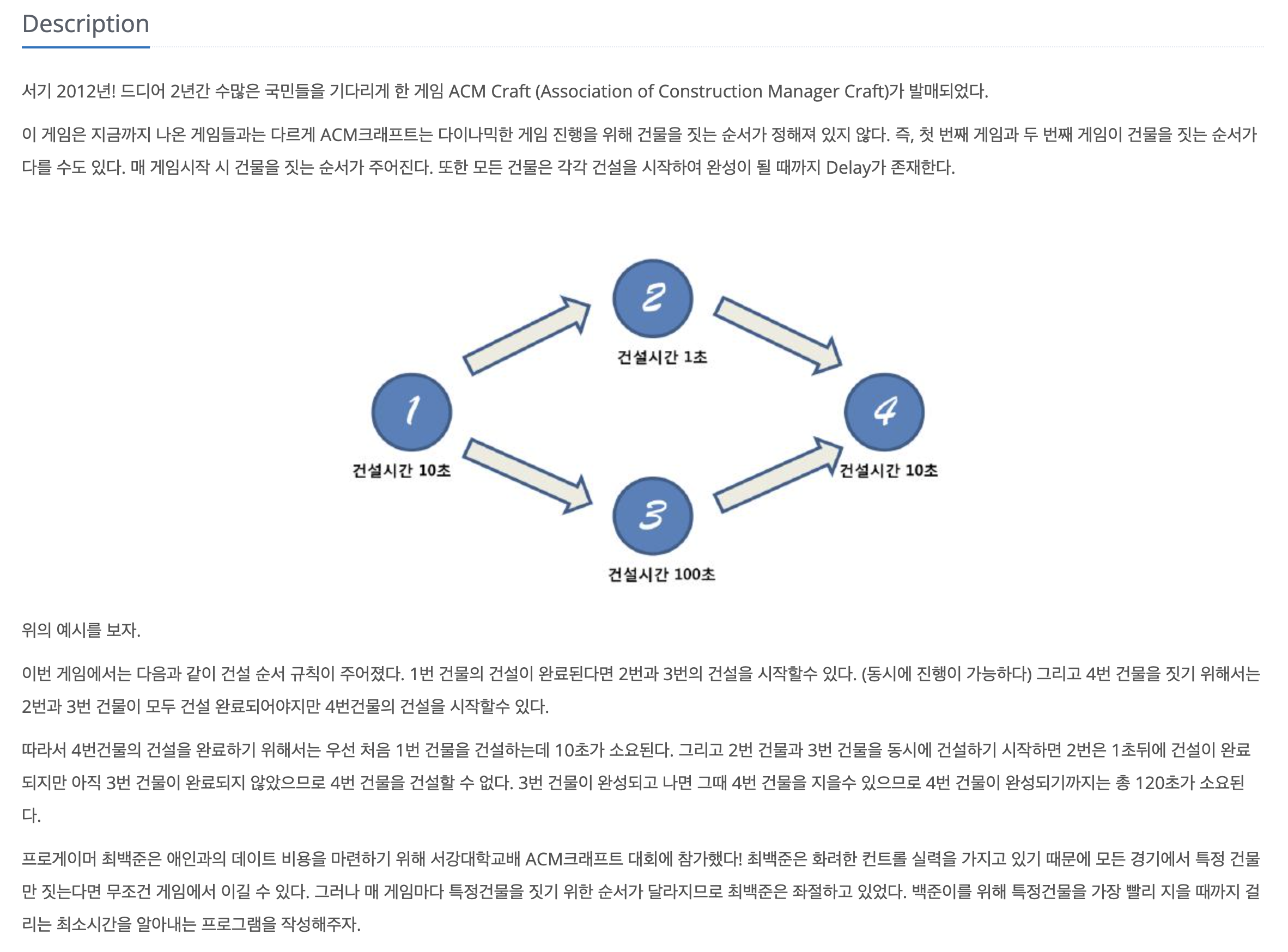
문제 설명
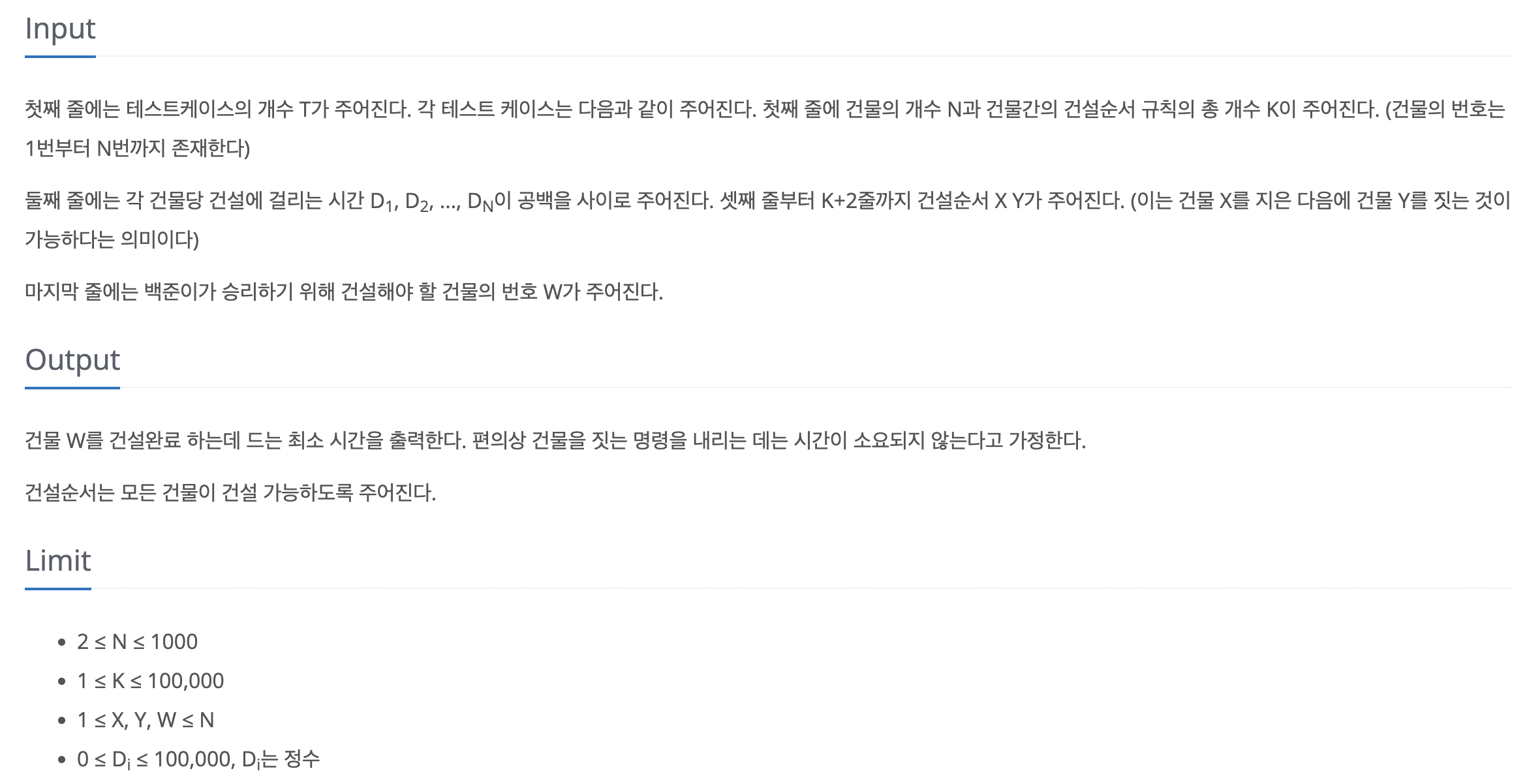
제한사항 및 입출력

내 풀이
문제를 똑바로 안 읽고 잘못 이해해서 이상한 방향으로 풀이하다가 애먹었다... 간단히 말하자면 목표 건물을 짓기까지 최소 시간인데, 건물들은 지을 때 필요한 선행 건물이 주어지고, 선행 건물들이 모두 지어져야 해당 건물을 건설할 수 있다. (하나만 지어져도 되는 줄...)
조건들을 요약해보면 다음과 같다.
- 건물 N개, 규칙 K개
- 규칙: {X}를 완성해야 Y를 착수 가능
- 각 건물의 공사 시간이 주어지고, 여러 건물을 동시에 공사할 수 있음
- 목표 건물 W를 가장 빨리 완성하기 위한 시간
관계에 사이클이 없으므로 그래프는 DAG를 성립한다. 선행 건물 관계가 이루는 DAG에서, 각 건물의 최소 완료 시간은 “선행들 중 가장 오래 걸리는 경로”를 기다린 뒤 자기 공사시간을 더한 값이다.
문제에서는 처리해야 할 순서가 주어지지 않고 “선행 -> 후행” 제약만 주어진다.(부분 순서) 우리가 순서를 스스로 만들어야하기 때문에 위상정렬을 이용하여 전파해주면 되겠다는 생각이 들었다. 아래 코드를 확인해보자.
코드
from collections import deque
import sys
input = sys.stdin.readline
mis = lambda: map(int, input().split())
INF = float('inf')
t = int(input())
for tc in range(t):
n, k = mis()
time = [0] + [*mis()]
graph = [[] for _ in range(n+1)]
indeg = [0] * (n+1) # 진입 차수
for _ in range(k):
a, b = mis()
graph[a].append(b)
indeg[b] += 1
w = int(input()) # 목표 건물
# dp[i] = i를 완성하는데 드는 최소시간
dp = [0] * (n+1)
# 진입차수 0부터 건물짓기
queue = deque()
for i in range(1, n+1):
if indeg[i] == 0:
dp[i] = time[i]
queue.append(i)
while queue:
x = queue.popleft()
for nx in graph[x]:
dp[nx] = max(dp[nx], dp[x] + time[nx])
indeg[nx] -= 1
if indeg[nx] == 0:
queue.append(nx)
print(dp[w])그래프를 구성해주면서 위상정렬을 위해 진입차수를 indeg에 저장한다. 이후 진입차수가 0인 노드부터 시작한다. 진입차수로 위상정렬을 진행하면서 모든 후행 노드에 대해 dp[nx] = max(dp[x], dp[x] + time[nx])를 계산한다. max 값으로 갱신하는 이유는 선행들 중 가장 오래 걸리는 시간을 측정하기 위함이다. 그리고 indeg[nx] -= 1 후 0이면 선행 건물이 모두 지어진 상황이기 때문에 큐에 삽입한다.
위 풀이가 성립하는 이유는 다음과 같다.
- 위상정렬 덕분에 모든 간선 u -> v에 대해 u가 항상 먼저 처리된다.
- 그러므로 v를 갱신할 때는 이미 u의 dp[u]가 확정되어 있고, v는 모든 선행을 본 뒤 그중 최댓값을 택하게 된다.
전파를 어떻게 할지만 잘 정한다면 어렵지 않게 풀이가 가능한 문제인 것 같다.

시간복잡도
각 노드와 간선을 한 번씩 처리하기 때문에 O(N + K)이다. 여기서 테스트케이스 T까지 고려한다면 O(T * (N+K))이다.
고찰
목표 W의 선행들을 거슬러 올라가며 가장 오래 걸리는 선행 경로의 완료시간을 메모이제이션하는 방식으로도 풀이가 가능하다. 따라서 그래프를 구성할 때 역방향으로 구성해주어야한다. 이렇게 풀이하는게 더 편한 것 같다...
import sys
mis = lambda: map(int, input().split())
input = sys.stdin.readline
sys.setrecursionlimit(10**5)
t = int(input())
for _ in range(t):
n, k = mis()
time = [0] + [*mis())
pred = [[] for _ in range(n+1)]
for _ in range(k):
a, b = map(int, input().split())
pred[b].append(a)
w = int(input())
dp = [-1] * (n+1)
@lru_cache(maxsize=None)
def dfs(v):
if not pred[v]:
return time[v]
return time[v] + max(dfs(u) for u in pred[v])
print(dfs(w))
@lru_cache 최고다...
'Computer Science > Problem Solving' 카테고리의 다른 글
| 백준 5624 - 좋은 수 (0) | 2025.09.01 |
|---|---|
| 백준 14607 - 피자 (Large) (0) | 2025.08.26 |
| 백준 12033 - 김인천씨의 식료품가게 (Small) (0) | 2025.08.22 |
| 백준 2176 - 합리적인 이동경로 (0) | 2025.08.20 |
| 백준 23326 - 홍익 투어리스트 (0) | 2025.08.19 |