문제설명

제한사항 및 입출력

풀이
문제의 제한사항을 확인해보면
1 <= k <= 5000
1 <= 던전의 개수 <= 8
으로 제한되어있다. 따라서 모든 던전의 순서를 확인해도 8!이기 때문에 굉장히 작은 것을 알 수 있다.
그러므로 간단하게 permutations을 활용하여 모든 경우의 수를 확인하고 가장 큰 값을 리턴하는 완전탐색으로 구현했다.
내 코드

가지 못하는 곳은 break를 해주면서 빠르게 제외시켜주었다. 실제로는 던전의 개수가 8개일 때 8!에 던전의 개수만큼 한 번 더 반복하기 때문에 8! * 8인 것을 확인할 수 있다. 약 32만이라는 작은 숫자이므로 간단하게 통과할 수 있었다.
고찰
내가 생각한 코드의 시간복잡도는 O(n * n!)로 매우 크다.
던전의 개수가 12개만 넘는다고 해도 5억에 가까운 숫자이므로 완전탐색은 힘들 수 있다.
1. 정렬을 활용한 그리디
사실 제일 처음 생각난 방법은 아니라 정렬한 후 "그리디하게 풀 수 있지 않을까?" 라는 생각이었다.
하지만 던전을 소모 피로도, 요구 피로도 어떤 걸 기준으로 정렬해도 최적을 보장하기 힘들다는 생각에 완전탐색으로 풀이하게 되었다.
2. 백트래킹 + 가지치기
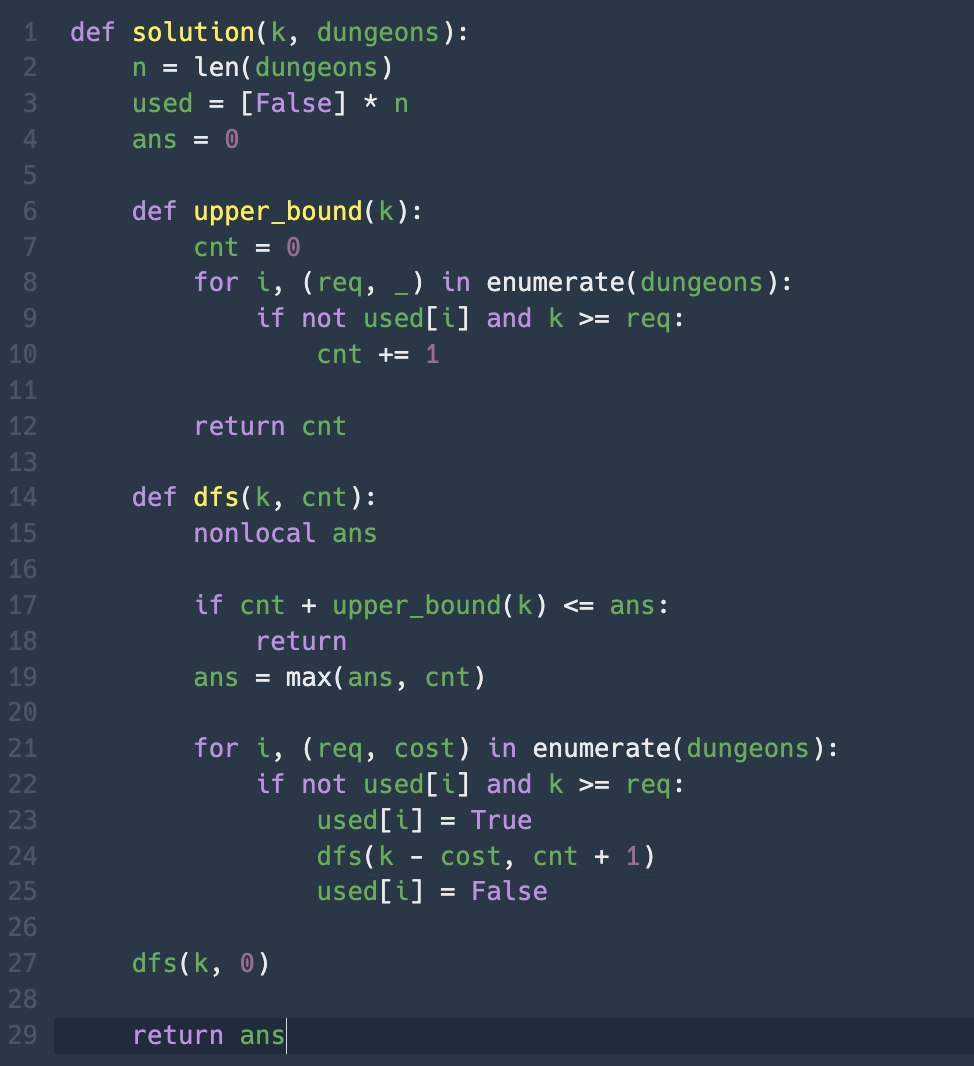
완전탐색을 구현함에 있어서 permutations이 직관적으로 구현하기 쉬워서 permutations을 활용한 코드로 작성했는데, 이번엔 백트래킹을 활용하여 풀이해보았다.
리스트를 활용하여 현재 상태를 복구하고 upper_bound 함수로 가지치기 했다.
upper_bound(k)는 “비용을 0이라고 가정하고, 지금 k로 요구치(req)만 충족하는 남은 던전 수”를 센다. 비용을 무시하므로 실제보다 많게 잡는다. 가지치기해도 최적해를 보장하기 위해 낙관적으로 잡았다.
가지치기의 핵심 로직은 cnt + upper_bound(k) <= best면, 이 분기에서 최대한 잘해도 현재 최고(best)를 넘을 수 없으니 탐색 중단하는 것이다.
시간복잡도는 똑같이 O(n * n!)이지만 가지치기로 인해 평균적인 통과 시간이 크게 줄었다. 근데 테스트케이스 8번에서는 오히려 늘었다...? 아마 최악의 경우 함수 호출로 인한 오버헤드가 있는 것 같다.
3. DP
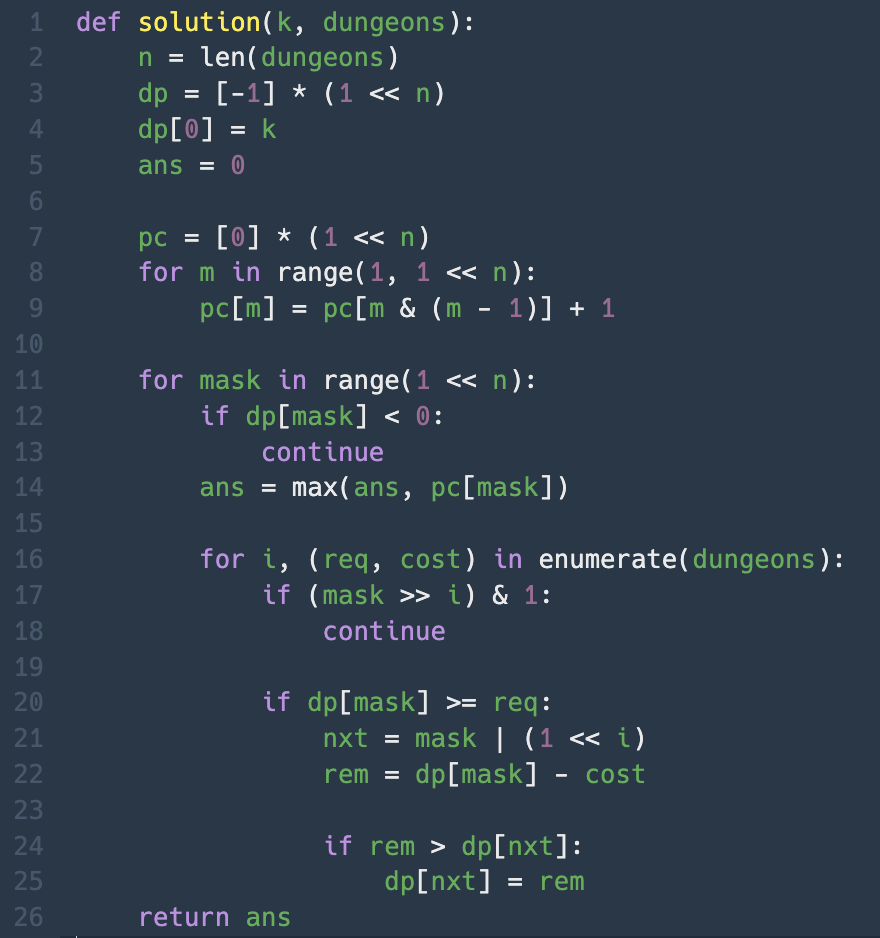
그 다음은 DP를 활용한 풀이이다. 일반적으론 상태를 저장하기가 껄끄러워 비트마스킹을 사용했다. 언제나 dp의 관건은 dp 테이블을 잘 정의하는 것이다.
나는 다음과 같이 dp를 정의했다.
mask(비트마스크): 지금까지 클리어한 던전의 수
dp[mask]: 그 집합을 어떤 순서로든 클리어하고 남길 수 있는 피로도의 최댓값 (불가능하면 -1)
핵심은 지금까지 어떤 던전을 클리어했는가(마스크)를 상태로 두고, 그 상태에서 남아있는 최대 피로도를 저장하는 것이다.
첫 번째 for문은 모든 상태를 순회하면서 저장된 가장 큰 값(ans)와 현재 마스크의 비트 개수(클리어한 던전의 수)를 비교하여 큰 값을 갱신한다. -> O(2^n)
두 번째 for문은 방문하지 않은 모든 던전들을 확인한다. -> O(n)
1. if (mask >> i) & 1: → i번째 비트가 1이면 이미 깬 던전이므로 패스.
2. 현재 남은 피로도 dp[mask]가 이 던전 요구치 req 이상이면 입장 가능
새 상태 nxt = mask | (1<<i) -> i번째 던전을 추가로 깬다면 새로 남을 피로도 rem = dp[mask] - cost
같은 nxt 상태에 도달하는 여러 경로 중 남은 피로도가 더 큰 rem > dp[nxt]일 때만 갱신한다.
시간복잡도는 O(n * 2^n)으로 팩토리얼에 비하면 엄청나게 감소했다.
전체적으로 통과시간이 크게 줄었다! 언제쯤 처음부터 이런 풀이를 생각할 수 있게 될까...
'Computer Science > Problem Solving' 카테고리의 다른 글
| 백준 23326 - 홍익 투어리스트 (0) | 2025.08.19 |
|---|---|
| 백준 13265 - 색칠하기 (0) | 2025.08.18 |
| 백준 15973 - 두 박스 (0) | 2025.08.18 |
| 백준 19622 - 회의실 배정 3 (0) | 2025.08.17 |
| 백준 9047 - 6174 (0) | 2025.08.17 |